KALKULUS 2 : Integral Fungsi Rasional Pangkat 1

INTEGRAL FUNGSI RASIONAL PANGKAT 1

Fungsi rasional dalah fungsi yang berbentuk pecahan dimana pembilang dan penyebutnya masing2 merupakan fungsi polinomial, fungsi rasional yang di maksud di sini adalah fungsi-fungsi yang berbentuk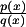

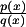dengan p(x) dan q(x) masing2 fungsi polinomial berderajat m dan n d imana m<n.

Teknik pengintegralan fungsi rasional didasarkan pada penguraian bentuk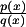

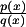menjadi bentuk yang lebih sederhana agar mudah untuk diiitegralkan berdasarkan faktor dari polinomial q(x).

Contoh: $\displaystyle \int \dfrac{2x+1}{x^2-3x+2} dx = \int \dfrac{2x+1}{(x-1)(x-2)} dx$

= $\displaystyle \int \dfrac{A}{x-1} dx + \int \dfrac{B}{x-2} dx$

A dan B dapat dicari melalui hubungan:

$\dfrac{2x+1}{x^2-3x+2} = \dfrac{A}{x-1} + \dfrac{B}{x-2}$

= $\dfrac{A(x-2)+B(x-1)}{(x-1)(x-2)}$

$\Leftrightarrow 2x + 1 = A(x-2) + B(x-1)$

$\Leftrightarrow 2x + 1 = (A + B)x - 2A - B$

$\Leftrightarrow (A + B) = 2$ dan $-2A - B = 1$

$\Leftrightarrow A = -3$ dan $B = 5$

= $\displaystyle \int \dfrac{-3}{x-1} dx + \int \dfrac{5}{x-2} dx$

misal : $u = x - 1 \Rightarrow du = dx$

$v = x - 2 \Rightarrow dv = dx$

= $\displaystyle \int \dfrac{-3}{u} du + \int \dfrac{5}{v} dv$

= $-3 \ln(u) + 5 \ln(v) + C$

= $-3 \ln(x-1) + 5 \ln(x-2) + C$

= $\ln \dfrac{(x-2)^5}{(x-1)^3} + C$

Aturan yang dapat dipedomani untuk penguraian bentuk $\dfrac{p(x)}{q(x)}$ sebagai berikut:

Untuk setiap faktor dari $q(x)$ berbentuk $(ax+b)^k$ , maka penguraian faktor tersebut berbentuk :

$\dfrac{A_1}{ax+b} + \dfrac{A_2}{(ax+b)^2} + \cdots + \dfrac{A_k}{(ax+b)^k}$
Untuk setiap faktor dari $q(x)$ berbentuk $(ax^2 + bx + c)^k$ , maka penguraian faktor tersbut berbentuk :

$\dfrac{A_1 x+B_1}{ax^2+bx+c} + \dfrac{A_2 x+B_2}{(ax^2+bx+c)^2} + \cdots + \dfrac{A_k x+B_k}{(ax^2+bx+c)^k}$

Agar lebih jelas tentang aturan tersebut, diberikan contoh berikut:

Contoh:

$\dfrac {2x^3+x^2+2x-1}{x^4-1}$ = $\dfrac{2x^3+x^2+2x-1}{(x-1)(x+1)(x^+1)}$

= $\dfrac{A}{x-1} + \dfrac{B}{x+1} + \dfrac{Cx+D}{x^2+1}$

dengan $A = B = D = 1$ dan $C = 0$
$\dfrac {3x^3 - 8x +13}{(x+3)(x-1)^2} = \dfrac {A}{x+3} + \dfrac{B}{x-1} + \dfrac{C}{(x-1)^2}$

dengan $A = 4, B = -1$ , dan $C = 2$
$\dfrac {6x^3 - 15x +22}{(x+3)(x^2-2)^2} = \dfrac {A}{x+3} + \dfrac{B}{x^2+2} + \dfrac{C}{(x^2-2)^2}$

dengan $A = 1, B = -1, C = 3 D = -5$ dan $E = 0$ .

Untuk kasus $n< m$ yaitu derajat polinomial $p(x)$ tidak kurang dari derajat polinomial $q(x)$ , maka sebelum diterapkan aturan penguraian di atas, perlu dilakukan penyederhanaan lebih dulu.

Contoh :

$\displaystyle \int \dfrac{x^3-1}{x^3+x} dx = \ldots$

Dalam hal ini $p(x) = x^3-1$ berderajat 3 dan $latex q(x) = x^3 + x$ juga berderajat 3.

$\displaystyle \int \dfrac{x^3-1}{x^3+x} dx = \int \left(1 + \dfrac{-1}{x} + \dfrac{x-1}{x^2+1} \right) ~dx$

= $\displaystyle \int 1 ~dx + \int \dfrac{-1}{x} ~dx + \int \dfrac{x-1}{x^2+1} ~dx$

= $\displaystyle \int 1 ~dx - \int \dfrac{1}{x} ~dx + \int \dfrac{x}{x^2+1} ~d \left( \dfrac{x^2+1}{2x} \right) - \int \dfrac{1}{x^2+1}$

= $\displaystyle \int 1 ~dx - \int \dfrac{1}{x} ~dx + \dfrac{1}{2} \int \dfrac{1}{x^2+1} ~d(x^2 + 1) - \int \dfrac{1}{x^2+1}~dx$

= $x - \ln x + \dfrac{1}{2} \ln(x^2 + 1) - \tan^{-1} x + C$

KALKULUS 2

Selasa, 24 Desember 2019

Integral Fungsi Rasional Pangkat 1

INTEGRAL FUNGSI RASIONAL PANGKAT 1

Tidak ada komentar:

Posting Komentar