INTEGRAL TENTU
Definisi
Jika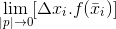 
ada maka fungsi f dapat diintegralkan pada selang a<x<b dan integral tentu f dari a ke b adalah sebagai berikut :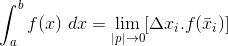 
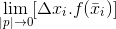ada maka fungsi f dapat diintegralkan pada selang a<x<b dan integral tentu f dari a ke b adalah sebagai berikut :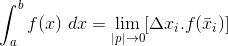
Teorema Dasar Kalkulus
Jika y = f(x) adalah fungsi kontinu pada selang a<x<b dan f(x) adalah sembarang anti turunan dari f(x) pada interval tersebut, maka berlaku bentuk berikut: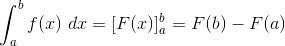 
rumus diatas menunjukan bahwa untuk menyelesaikan integral tentu adalah dengan mengintegralkan f(x) terlebih dahulu, kemudian substitusi batas atas integral dan hasilnya kurangi dengan hasil substitusi batas bawah integral.
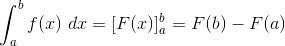rumus diatas menunjukan bahwa untuk menyelesaikan integral tentu adalah dengan mengintegralkan f(x) terlebih dahulu, kemudian substitusi batas atas integral dan hasilnya kurangi dengan hasil substitusi batas bawah integral.
Sifat-Sifat Integral Tentu
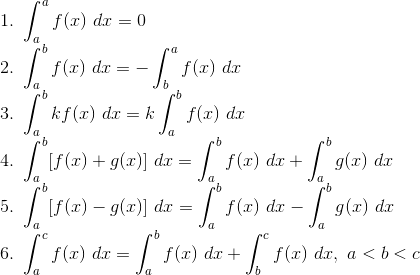
Contoh Soal dan jawaban:
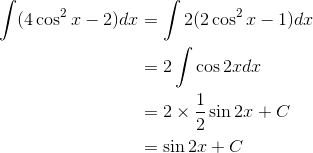
Tidak ada komentar:
Posting Komentar